Next: Crystal Field and Parameter Up: McPhase USERS MANUAL Previous: DyNiBC - single ion Contents Index
The crystal field ground state of the ![]() Er
Er![]() ion in ErNi
ion in ErNi![]() B
B![]() C
can be described by a quasi-quartett consisting of two doublets separated
by a energy interval
C
can be described by a quasi-quartett consisting of two doublets separated
by a energy interval ![]() .
.
In order to calculate efficiently the single ion property (for small effective
magnetic fields in comparison to the total CF splitting) the
Hamiltonian
![]() is projected to the quasi quartett
and may be written as
is projected to the quasi quartett
and may be written as
with the angular momentum operators given by the 4x4 matrices
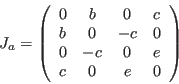 |
(167) |
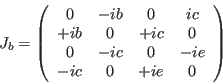 |
(168) |
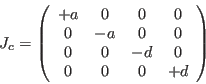 |
(169) |
The constants ![]() -
-![]() can be computed from the crystal field parameters, if
these are known. On the other hand, they are connected to the saturation
magnetic moments
can be computed from the crystal field parameters, if
these are known. On the other hand, they are connected to the saturation
magnetic moments ![]() by the following equations (
by the following equations (![]() denotes the
maximum of the argument values)
denotes the
maximum of the argument values)
| (170) |
| (171) | |||
| (172) |
| (173) | |||
| (174) |
The module given in /examples/erni2b2c/1ion_mod/quartett.c diagonalises
the Hamiltonian (175) and calculates the thermal expectation
value ![]() of the vector
of the vector ![]() , which
is returned to the McPhas program.
, which
is returned to the McPhas program.