Next: Mixing term Up: Crystal Field Phonon Interaction Previous: Crystal Field Phonon Interaction Contents Index
The elastic energy ![]() is bilinear in
is bilinear in ![]()
We calculate it's derivative with respect to
![]() :
:
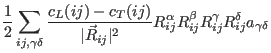 |
|||
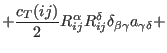 |
|||
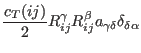 |
(80) |
we make use of the fact that the strain ![]() is a symmetric
tensor (
is a symmetric
tensor (
![]() ) and a rotation
is antisymmetric (
) and a rotation
is antisymmetric (
![]() ) and
the linear transformation
) and
the linear transformation ![]() can be written as
can be written as
![]() . Thus
derivatives with respect to the strain component
. Thus
derivatives with respect to the strain component
![]() with
with
![]() can be written as
can be written as
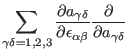 |
(81) | ||
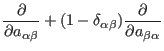 |
(82) |
We calculate the derivative of the elastic energy with respect to the strain:
An we make also use of the definition of elastic constants to find
and rewrite the elastic energy in the well known fashion
Note that we have neglected the fact, that nonzero transversal springs will
result in a dependence of the elastic energy on the rotation tensor ![]() as
can been seen by inserting a rotation into the second part of (83).
14
Therefore transversal springs have to be used with caution
in the description of a phonon spectrum.
as
can been seen by inserting a rotation into the second part of (83).
14
Therefore transversal springs have to be used with caution
in the description of a phonon spectrum.
With the help of elastic constants we can rewrite the derivative of the elastic energy (87), again ignoring the rotation dependence:
To easy the indexing we apply the notation of Voigt
Note the elastic constants do not contain any prefactor in Voigt notation, i.e.
There are 21 independent elastic constants,
![]() with
with ![]() and
and
![]() . The other 60 elastic constants
can be obtained from the symmetry relations
. The other 60 elastic constants
can be obtained from the symmetry relations
![]() ,
,
![]() .
.
The elastic energy in Voigt notation is given by